(Colégio Naval 2021) Marque a opção que apresenta a solução da inequação abaixo.
a) S = { x ∈ R | -1 < x < 0}
b) S = { x ∈ R | -4 < x < -1 U 0 < x < 2 }
c) S = { x ∈ R | 2 < x < 4}
d) S = { x ∈ R | -8 < x < -4}
e) S = { x ∈ R | -1 < x < 0 U 0 < x < 2 }
Solução: questão de matemática do Concurso Público de Admissão ao Colégio Naval (CPACN/2021). Prova aplicada no dia 02/10/2021.
Para resolvermos essa inequação quociente, vamos nomear:
N(x) o polinômio do numerador:
D(x) o polinômio do denominador.
De modo que teremos: N(x) / D(x) < 0
Simplificando esses dois polinômios, chegaremos a:
x² + 4x < 0
x² - x -2
Perceba que ambos são do segundo grau, com coeficiente "a" positivo, logo possuem formato de parábola com concavidade voltada para cima (formato de U ). Vamos encontrar suas raízes e esboçar seus gráficos para analisarmos os pontos positivos e negativos que os resultados de cada polinômio pode assumir em função de x.
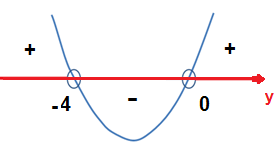
>>> N(x)
x² + 4x = 0
x ( x + 4) = 0
x = 0 ou x = -4
Esboço gráfico
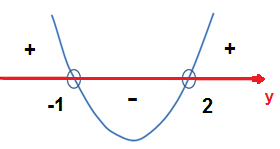
>>> D(x)
x² - x -2 = 0
Δ = b² - 4ac
Δ = (-1)² - 4(1)(-2)
Δ = 1 + 8
Δ = 9
√Δ = 3
x = (-b ± √Δ) / 2a
x = (1 ± 3) / 2
x = 2 ou x = -1
Esboço Gráfico
Agora, vamos plotar todos esses pontos no mesmo esboço gráfico e encontrar os sinais para N(x)/D(x). Atente que quando ambos são positivos ou ambos são negativos, o resultado N(x)/D(x) será positivo. Já quando eles possuem sinais contrários o resultado N(x)/D(x) é negativo.
Alternativa correta é a letra b).
Aproveite e continue praticando com uma lista de questões anteriores do Colégio Naval.
Um forte abraço e bons estudos.