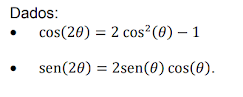(UNICAMP 2022) No dia 23 de março de 2021, um navio encalhou no canal de Suez, no Egito. A embarcação tinha 400 metros de comprimento e 60 metros de largura. No ponto onde aconteceu o acidente, o canal de Suez não tem mais do que 200 metros de largura. Abaixo apresentamos uma foto de satélite e uma figura representando a situação. O ângulo 𝛼 indicado na figura abaixo mede 67,5°.




A largura do canal, medida em metros e indicada por 𝐿 na figura anterior, é:

Solução: questão de matemática do Vestibular UNICAMP 2022. Prova aplicada no dia 07/11/2021.

Uma questão muito interessante e contextualizada de matemática onde utilizaremos muito a disciplina trigonometria. Para resolver este problema, vamos ilustrar alguns pontos importantes:




Repare que os ângulos ACB, ABE e BED medem 90°, o ângulo ABC vale (90°- α) e por conseguinte o ângulo CBE vale α.

Nosso objetivo é encontrar L, podemos fazer isso por meio do triângulo retângulo BED.  Temos que:

cos α = BE / BD
cos α = L / (BC + CD)

Sabemos que CD vale 400, atualizando: 

cos α = L / (BC +400)

BC . cos α  + 400 . cos α  = L   (Equação I)

Quanto vale BC?  Podemos encontrá-lo usando as relações trigonométricas no triângulo retângulo ABC.

tg α = BC/AC
tg α = BC/30
BC = 30 . tg α  (Equação II)

Vamos aplicar este valor de BC na Equação I.

L = BC . cos α  + 400 . cos α
L = 30 . tg α . cos α  + 400 . cos α
L = 30 . (sen α/cos α) . cos α  + 400 . cos α
L = 30 . sen α + 400 . cos α

Agora, precisamos encontrar os valores de seno e cosseno de  α = 67,5°.

Sabemos que 2 x α = 2 x 67,5° = 135°.

cos 135° = - cos 45° = -√2/2
sen 135° = sen 45° = √2/2

Vamos usar as fórmulas dos arcos duplos informadas no enunciado para encontrar seno e cosseno de α por meio do conhecimento do seno e cosseno de 2α.

cos (2α) = 2 cos²(α) - 1
cos (2α) + 1 = 2 cos²(α)
cos²(α) = [ cos (2α) + 1 ] / 2
cos(α) = ± √[ (cos (2α) + 1)/2 ]

Como α é um ângulo do primeiro quadrante, então seu cosseno é positivo e ficamos com:

cos(α) = √[ (cos (2α) + 1)/2 ]

Agora, aplicamos o valor de α


Agora, vamos para o seno:

sen (2α) = 2 senα cosα
senα = sen (2α) / 2.cosα 

Agora, aplicamos o valor de α



Finalmente, podemos encontrar L

L = 30 . sen 67,5° + 400 . cos 67,5°
L = 30 . [ (1/2) . √(2+√2) ] + 400 . [ (1/2) . √(2-√2) ]
L = 15√(2+√2) + 200 . √(2-√2)
 
Alternativa correta é a letra c).

Aproveite e continue praticando com uma lista de questões anteriores da UNICAMP.

Um forte abraço e bons estudos.