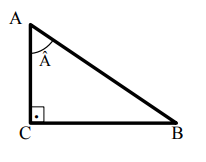
(ESA 2024) Em um triângulo retângulo ABC, com ângulo reto em C, sabe-se que tg  = 2. Marque a alternativa que representa o valor de sen Â.

a) sen  = 2√5
                         3

b) sen  = 3√5
                         3

c) sen  = 2√5
                         5

d) sen  = 3√5
                         5

e) sen  = 3√5
                         7
Solução: questão de matemática da ESA (Escola de Sargentos das Armas) do Concurso de Admissão 2023 aos Cursos de Formação e Graduação de Sargentos 2024 – 25 . Prova aplicada em 08/10/2023.

O enunciado nos informa que  tg  = 2.  Sabemos que

tg  = CB/AC
2 = CB/AC
CB = 2·AC

Ou seja, CB mede o dobro de AC, portanto, vamos atribuir para AC o valor de x e para CB o valor de 2x.  



Agora, vamos utilizar o Teorema de Pitágoras para encontrar quanto mede AB.

AB² = AC² + CB²
AB² = x² + (2x)²
AB² = x² + 4x²
AB² = 5x²
AB = x√5

Atualizando a figura:



Cálculo de sen Â

sen Â = CB/AB
sen Â = (2x)/(x√5)
sen Â = 2/√5
Racionalizar por (√5)/(√5)
sen Â =  2  ·  √5 
                √5     √5

sen Â =  2√5 
                     5 

Alternativa correta é a letra c).

Aproveite e continue praticando com uma lista de questões anteriores da ESA.

Um forte abraço e bons estudos.