(SEEDUC-RJ 2015 - Banca CEPERJ) Resolvendo corretamente a equação trigonométrica 2 sen(2x) = sen (x), x ∈ [0, 2π], determina-se o conjunto solução com exatamente t elementos. O valor de t é igual a:

(Professor Docente I - Matemática - 2015 - Banca CEPERJ)  Resolvendo corretamente a equação trigonométrica 2 sen(2x) = sen (x), x ∈ [0, 2π], determina-se o conjunto solução com exatamente t elementos.  O valor de t é igual a:

a) 1  b) 2  c) 3  d) 4  e)  5

Solução:    questão do concurso para professor de matemática da Secretaria de Educação do Rio de Janeiro.  Banca organizadora CEPERJ, 2015.

Na equação trigonométrica:

2 sen(2x) = sen (x)

Vamos substituir sen(2x) por 2sen(x).cos(x)

2 . 2sen(x)cos(x) = sen(x)

4 sen(x)cos(x) - sen(x) = 0

sen(x) [4cos(x) - 1] = 0

sen(x) = 0  ou  4 cos(x) - 1 = 0

Nesta questão sobre equações trigonométricas, temos que atentar para o fato do ângulo x estar limitado no intervalo  [0, 2π].

Neste intervalo, existem 3 ângulos que satisfazem sen(x) = 0 . Vamos esboçar o ciclo trigonométrico.

Os ângulos x= 0, π e 2π satisfazem a equação trigonométrica, vejamos:

x = 0  ;   sen(0) = 0 ; sen(2.0) = 0

2. 0 = 0  (Satisfaz)

x = π ;    sen(π) = 0 ; sen(2.π)=0

2. 0 = 0  (Satisfaz)

x = 2π ;   sen(2π) = 0 ; sen(2.2π)=0

2. 0 = 0  (Satisfaz)

Além destas três soluções, existem outras duas, quando 4 cos(x) - 1 = 0

4 cos(x) = 1

cos (x) = 1/4

x = arccos (1/4)

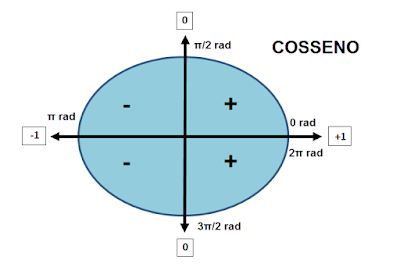
No intervalo [0, 2π] o cosseno de x assume valor de 1/4 em duas ocasiões, no primeiro e no quarto quadrante.  

Então, são mais 2 soluções, que somadas às 3 primeiras, totalizam 5 soluções.

Alternativa correta é a letra E.

Curiosidade:  não é necessário, para responder a esta questão, especificar quais são as duas soluções dadas por arccos(1/4).  Basta visualizar que existem dois ângulos que satisfazem a condição dentro do intervalo [0, 2π]. Entretanto, por curiosidade e com ajuda do Excel chegamos aos ângulos 1,318116072 radianos e 4,965069236 radianos.  Em graus, eles valem aproximadamente 75,52º e 284,47°.

Aproveite e continue praticando com uma lista de questões resolvidas de trigonometria e identidades trigonométricas.

Um forte abraço e bons estudos.