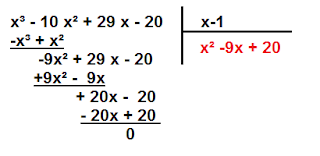(Escola de Aprendizes-Marinheiros 2020) As raízes do polinômio p(x) = x³ - 10 x² + 29 x - 20 são as dimensões de um paralelepípedo retângulo. É correto afirmar que a área de todas as faces da figura em unidades de área é igual a:
a) 28 b) 29 c) 36 d) 48 e) 58
Solução: questão de matemática do Concurso Público de Admissão às Escolas de Aprendizes-Marinheiros/CPAEAM/2020. Para resolvê-la, precisamos obter as raízes (x1,x2 e x3) do polinômio p(x) e depois calcular a área lateral de um paralelepípedo retângulo de medidas (x1, x2 e x3).Primeiramente, vamos obter as raízes do polinômio p(x). Perceba que 1 é uma raiz desse polinômio, então p(x) é divisível por (x-1). Procedemos a divisão de x³ - 10 x² + 29 x - 20 por (x-1).
> a soma das raízes = -b/a = -(-9)/1 = 9
> o produto das raízes = c/a = 20
As raízes são: 4 e 5, pois 4+5 = 9 e 4.5 = 20.
As raízes de p(x) são {1, 4 e 5} e as dimensões do paralelepípedo retângulo também.
Área Lateral (AL) = 2 x (4x5) + 2 x (1x5) + 2 x (1x4)
AL = 2 x (20) + 2 x (5) + 2 x (4)
AL = 40 + 10 + 8 = 58 unidades de área.
Alternativa correta é a letra e).
Aproveite e continue praticando com uma lista de Exercícios Resolvidos de Polinômios e Equações Polinomiais.
Um forte abraço e bons estudos.