(EEAR CFS 1/2022) Sejam os arcos de 480° e −4π/3 rad. No ciclo trigonométrico, esses arcos são tais que ambos estão no
a) 1º quadrante e são côngruos.
b) 2º quadrante e são côngruos.
c) 1º quadrante e não são côngruos.
d) 2º quadrante e não são côngruos.
Solução: questão de matemática da EEAR (Escola de Especialistas da Aeronáutica) do Exame de Admissão ao CFS 1/2022. Prova aplicada no dia 30/05/2021.
Nesta questão, utilizaremos conceitos da trigonometria dentro de um ciclo trigonométrico. Em primeiro lugar, vamos converter o ângulo −4π/3 rad para graus.
-4 . 180°/3
-4. 60°
- 240°
Agora, vamos dividir o ângulo 480° por 360°, encontraremos como resultado quociente igual a 1 e resto igual a 120°.
480° = 1 x 360° + 120°
Ou seja, o 480° dá uma volta completa no ciclo e depois termina sobre o ângulo de 120°. Os arcos 480° e 120° são côngruos.
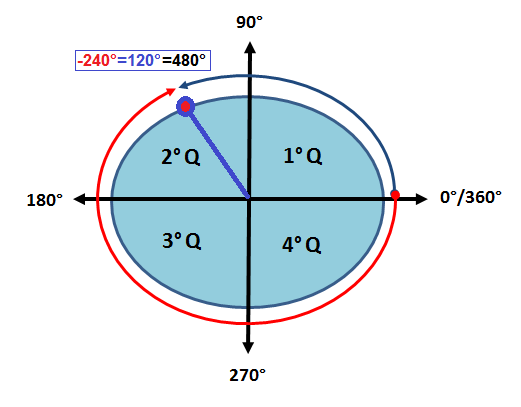
Atenção: no ciclo trigonométrico, os ângulos positivos giram no sentido anti-horário. Já os ângulos negativos, giram no sentido horário. Vamos ilustrar no ciclo trigonométrico os ângulos -240° e 480°.
Perceba que os arcos de 480° e -240° são côngruos (possuem origem e destino iguais) e estão no 2° quadrante.
Alternativa correta é a letra b).
Aproveite e continue praticando com uma lista de questões anteriores da EEAR.
Um forte abraço e bons estudos.