(FAMEMA 2022) Uma pirâmide quadrangular regular, de vidro maciço, tem todas as arestas de 6 cm de comprimento. Sabe-se que a densidade do vidro é de 2,5 g/cm³ . Considere √2 = 1,41.
A massa, em gramas, dessa pirâmide de vidro é, aproximadamente,
(A) 120. (B) 127. (C) 133. (D) 140. (E) 158.
Solução: questão de matemática do Vestibular da Faculdade de Medicina de Marília, ano: 2022, banca examinadora: FGV. Prova aplicada no dia 05/12/2021.
Em primeiro lugar, vamos calcular o volume (Vp) dessa pirâmide.
A fórmula do volume da pirâmide quadrangular regular é igual a:
Vp = (1/3) . Área da Base x altura
Vp = (1/3) . 6² . altura
Vp = (1/3) . 36 . altura
Vp = 12 . altura
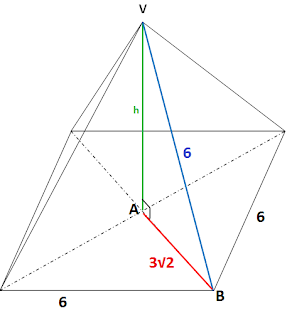
Podemos encontrar a altura (h) dessa pirâmide aplicando o Teorema de Pitágoras no triângulo retângulo VAB, repare na ilustração a seguir:
VA representa a altura (h) da pirâmide
AB representa metade da diagonal de um quadrado de lado 6, sabemos que a diagonal vale
lado√2 = 6√2. A metade de 6√2 é igual a 3√2.
VB é uma das arestas dessa pirâmide, logo mede 6.
Aplicando o Teorema de Pitágoras, temos que:
VA² + AB² = VB²
h² + (3√2)² = 6²
h² + 9.2 = 36
h² = 36 - 18
h² = 18
h = 3√2 (e aplicamos este valor na fórmula do volume)
Vp = 12 . altura
Vp = 12 . 3√2
Vp = 36√2
Do enunciado (√2 = 1,41)
Vp = 36 . 1,41
Vp = 50,76 cm³
Finalmente, vamos calcular a massa. Sabemos que densidade = massa / volume
2,5 g/cm³ = massa / 50,76 cm³
2,5 g/cm³ . 50,76 cm³ = massa
2,5 g . 50,76 = massa
massa = 126,9 g ≅ 127 g
Alternativa correta é a letra b) .
Aproveite e continue praticando com uma lista de questões anteriores da FAMEMA.
Um forte abraço e bons estudos.