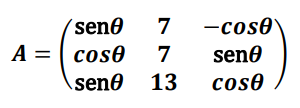(UFPR 2022) Considere a seguinte matriz:
Assinale a alternativa que corresponde à soma dos valores de θ ∈ [0, π] que satisfazem det A = -13.
a) π/4
b) 2π/3
c) 3π/4
d) 2π
e) 4π
Solução: questão de matemática do Vestibular UFPR 2022, prova do dia 13/02/2022.
Uma questão bem rica sobre determinantes e identidades trigonométricas. Em primeiro lugar, vamos calcular o det A e igualar a -13. Para encontrar este determinante, vamos usar a regra de Sarrus.
7senθcosθ - 13 sen²θ - 7 cos²θ + 7senθcosθ + 7sen²θ - 13 cos²θ
Agora, vamos re-organizar e simplificar
7senθcosθ + 7senθcosθ - 13 sen²θ - 13 cos²θ - 7 cos²θ + 7sen²θ
14senθcosθ - 13 (sen²θ + cos²θ) - 7 (cos²θ - sen²θ)
Sabemos que sen²θ + cos²θ = 1
14senθcosθ - 13 (1) - 7 (cos²θ - sen²θ)
7 . 2senθcosθ - 13 - 7 (cos²θ - sen²θ)
Sabemos que
sen 2θ = 2senθcosθ
cos 2θ = cos²θ - sen²θ
Sendo assim,
7 . 2senθcosθ - 13 - 7 (cos²θ - sen²θ)
7 . sen 2θ - 13 - 7 cos 2θ
Agora, vamos igualar este valor de det A ao valor de -13.
7 . sen 2θ - 13 - 7 cos 2θ = -13
7 . sen 2θ - 7 cos 2θ = -13 + 13
7 . sen 2θ - 7 cos 2θ = 0
7 . sen 2θ = 7 cos 2θ
sen 2θ / cos 2θ = 7/7
Sabemos que tg 2θ = sen 2θ / cos 2θ
sen 2θ / cos 2θ = 7/7
tg 2θ = 1
Agora, precisamos ter em mente que a tangente de um ângulo valerá +1 no primeiro e no terceiro quadrante, quando este ângulo valer 45º ou 225º. Ou seja,
2θ = 45° + N . 180º
Vamos escrever isto em radianos, sabemos que 180° = π e que 45º = π/4.
2θ = π/4 + N . π
θ = π/8 + N . (π/2)
Vamos verificar agora quais valores são válidos, dada a condição de que θ ∈ [0, π].
Quando N = 0
θ = π/8 + 0 . (π/2)
θ = π/8 (valor válido, pois θ está no intervalo [0, π] )
Quando N = 1
θ = π/8 + 1 . (π/2)
θ = π/8 + π/2 = π/8 + 4π/8 = 5π/8 (valor válido, pois θ está no intervalo [0, π] )
Quando N = 2
θ = π/8 + 2 . (π/2)
θ = π/8 + π = 9π/8 (valor inválido, pois θ está fora do intervalo [0, π] )
Quando N ≥ 2 os valores de θ estarão fora do intervalo dado no enunciado.
Portanto, o conjunto solução só possui os elementos {π/8 e 5π/8}.
Finalmente, a soma dos valores de θ ∈ [0, π] que satisfazem det A = -13, será igual a
π/8 + 5π/8 = 6π/8 = 3π/4
Alternativa correta é a letra c).
Aproveite e continue praticando com uma lista de questões de matemática da UFPR.
Um forte abraço e bons estudos.