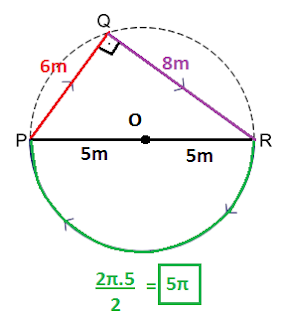
(VUNESP 2023) Observe a figura, formada por um triângulo PQR inscrito
em uma circunferência de diâmetro PR = 10 m, em que
PQ = 6 m. Uma partícula se move sobre a linha contínua,
iniciando seu movimento em P, passando por Q, depois
por R e, finalmente, voltando a P, como mostram as setas
sobre a trajetória.
A partícula parte de P com velocidade inicial de 8 m/s, e o
módulo de sua velocidade aumenta uniformemente ao longo
da trajetória, até chegar novamente em P, com velocidade
de 10 m/s. Adotando π = 3, o módulo da aceleração escalar
dessa partícula ao longo de todo seu percurso é de:
a) 36/89 m/s²
b) 3/25 m/s²
c) 2/11 m/s²
d) 18/29 m/s²
e) 1/11 m/s²
Solução: questão de matemática do Vestibular UNESP 2023, prova aplicada no dia 15/11/2022.
Note que o triângulo PQR está inscrito na circunferência e o seu lado PR é também o diâmetro da circunferência. Sabemos que quando isso ocorre, o triângulo PQR é retângulo, o ângulo reto está em Q, sendo PR a hipotenusa e PQ e QR seus catetos. Vamos atualizar a figura.
Note que PR = 10m, PQ = 6m e QR pode ser obtido pelo Teorema de Pitágoras, ou identificando que estamos diante de um triângulo retângulo com medidas proporcionais a 3-4-5.
PR² = PQ² + QR²
10² = 6² + QR²
QR² = 64
QR = 8 m
Além disso, como o diâmetro da circunferência vale 10 m, então o raio vale 5m, ou seja, a metade. Note que o trajeto feito no trecho de R até P, ilustrado em verde, tem medida de meia circunferência. Sabemos que a fórmula do comprimento de uma circunferência é dado por
2π . raio
2π . 5
10π
Como queremos a metade disso, então basta dividir por 2 e teremos 10π/2 = 5π m.
Já podemos calcular a distância (ΔS) percorrida pela partícula:
ΔS = 6 + 8 + 5π
Adotando π = 3
ΔS = 14 + 5.3
ΔS = 29 m
Além disso, o enunciado estabelece que "a partícula parte de P com velocidade inicial de 8 m/s, e o módulo de sua velocidade aumenta uniformemente ao longo da trajetória, até chegar novamente em P, com velocidade de 10 m/s."
Note que estamos diante de um MUV (movimento uniformemente variado) onde a velocidade está variando no percurso a uma taxa constante, ou seja, a aceleração é constante e diferente de zero.
Destacamos também as seguintes informações:
Velocidade inicial (Vo) = 8 m/s.
Velocidade final (V) = 10 m/s.
Finalmente, podemos encontrar o módulo da aceleração escalar dessa partícula ao longo de todo seu percurso utilizando a Equação de Torricelli.
V² = Vo² + 2aΔS
10² = 8² + 2a.29
100 - 64 = 2 . 29 . a
36 = 2 . 29 . a
18 = 29 . a
a = 18/29 m/s²
Alternativa correta é a letra d).
 Observe a figura, formada por um triângulo PQR inscrito em uma circunferência de diâmetro PR = 10 m, em que PQ = 6 m. Uma partícula se move sobre a linha contínua, iniciando seu movimento em P, passando por Q, depois por R e, finalmente, voltando a P, como mostram as setas sobre a trajetória.){kind=link}
0 Comentários