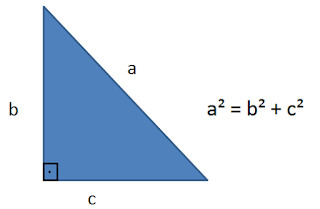
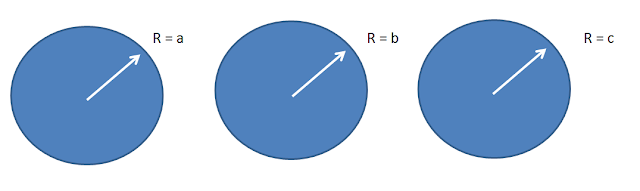(CEDERJ 2019.2) A respeito de um triângulo retângulo cuja medida da hipotenusa é a e cujos catetos medem, na mesma unidade de comprimento, b e c, considere as três afirmações:

I  Sendo T1, T2 e T3 triângulos equiláteros de perímetros 3a, 3b e 3c, respectivamente, a área de T1 é igual à soma das áreas de T2 e T3.

II  A área de um círculo, C1, de raio com medida a é igual à soma das áreas de dois círculos, C2 e C3, cujos raios medem b e c, respectivamente.

III A área de um quadrado cujo lado mede a é igual a área do quadrado cujo lado mede ( b + c ).

É verdadeiro o que é afirmado apenas em

a) I
b) I e II
c) II e III
d) III

Solução:  questão bem interessante do vestibular CEDERJ 2019.2 sobre áreas de figuras planas.    Temos que ter em mente a seguinte relação do teorema de Pitágoras.



Agora vamos julgar item a item:

Afirmativa I

Vamos testar se T1 = T2 + T3

A fórmula da área de um triângulo equilátero é lado² x √3/4

 a² √3/4 = b² √3/4  + c²√3/4
a² √3/4 = √3/4 (b²+ c²)
a² = b² + c ²   (Verdade.)

 Afirmativa II



Vamos testar se Ac1 = Ac2 + Ac3

A área de um círculo é dada por π x R²

π a² = π b² +  π c²
π a² = π (b² + c²)
a² = b² + c²    (Verdade.)

 Analisando as opções de resposta, já teríamos elementos suficientes para marcar a letra (b), mesmo assim, vamos testar a última proposição.

 Afirmativa III
Vamos testar se A1 = A2
A área do quadrado é dada por lado x lado.

 a² = (b+c)²
a² = b² + 2bc + c² 
Esta afirmativa é falsa, pois já sabemos que a² = b² + c²

Portanto, a alternativa correta é a letra B.

Aproveite e confira mais questões sobre áreas de figuras planas. 

 Um forte abraço e bons estudos.