(EPCAR 2021) Na EPCAR, durante o ano letivo, os alunos das três séries se enfrentam em uma competição esportiva denominada “Troféu Tenente Lima Mendes”. 

Para o ano de 2021, o comandante ordenou que fosse construído um novo pódio no qual a posição mais alta tenha forma de um cubo e as posições inferiores tenham forma de paralelepípedos retos retângulos conforme figura abaixo, com dimensões indicadas numa mesma unidade de medida.




Depois de construído em sua totalidade, o pódio deverá ser pintado, com exceção da parte inferior que estará apoiada no solo.

A expressão que melhor representa a área a ser pintada, em função de x, em unidade de área, é 

a) (35 x²) / 6

b) (67 x²) / 12

c) (11 x²) / 2

d) (23 x²) /2

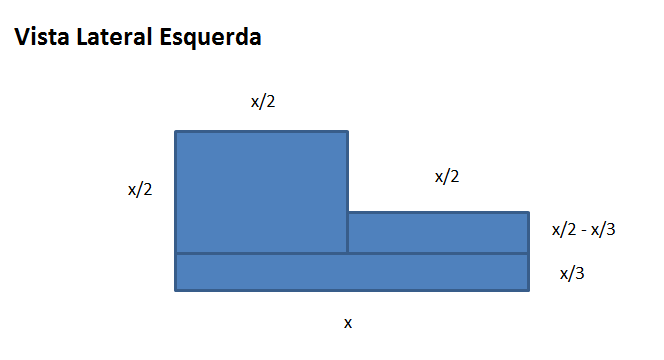
Solução:  nesta questão de geometria, vamos trabalhar o seu desenvolvimento em partes.   Podemos visualizar nosso problema tridimensional por meio de várias figuras de duas dimensões, são  elas:  vista frontal (Vf), vista traseira (Vt), vista lateral esquerda (Vle), vista lateral direita (Vld) e vista superior (Vs).  Para calcularmos a área total a ser pintada (At) vamos calcular a área de todas as vistas e depois somá-las.  



Área de Vf ou simplesmente Vf será calculada pela soma da área de todas as três figuras acima.  É um cálculo muito simples, basta fazer o produto da base pela altura.

Vf = (x/2 . x/2) + (x/3 . x) + (x . x/2)
Vf = (x²/4) + (x²/3) + (x²/2)
Vf = (13/12) . x²

Nas próximas vistas, vamos omitir esses cálculos e exibir apenas o resultado final das áreas. Como exercício você pode calcular e confrontar com os valores informados.  



Vt = (13/12) . x²



Vle = (2/3) . x²




Vld = (2/3) . x²



Vs = 2x²


Finalmente At = Vf + Vt + Vle  + Vld  + Vs
At = (13/12) . x² + (13/12) . x² + (2/3) . x² + (2/3) . x² + 2x²
At = 11/2 x²  [ alternativa correta é a letra C]

Espero que esta resolução passo a passo e ilustrada tenha te ajudado a compreender a solução desta questão e te ajude em sua preparação para vestibular, concurso ou carreiras militares.  

Está estudando geometria? Então aproveite e confira também:

>>  Lista de exercícios de Áreas de Figuras Planas;

>>  Lista de exercícios de Geometria Espacial;


Um forte abraço e bons estudos.