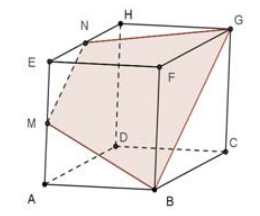
(Professor Docente I - Matemática - SEEDUC-RJ - 2015 - Banca CEPERJ) Um cubo ABCDEFGH foi seccionado por um plano MNGB, sendo M e N respectivamente os pontos médios das arestas AE e EH. A figura abaixo representa o cubo e a secção.
Se a medida de cada aresta desse cubo é 2 cm, a área, em cm² , do quadrilátero MNGB é igual a:
A) 4,5 B) 4,8 C) 5,0 D) 5,2 E) 5,6
Solução: questão do concurso para professor de matemática da Secretaria de Educação do Rio de Janeiro. Banca organizadora CEPERJ, 2015. Podemos encontrar as medidas do quadrilátero usando o Teorema de Pitágoras, repare na figura a seguir:.B = base maior; b = base menor; e h = altura. Repare na figura a seguir.
A altura pode ser obtida por meio do Teorema de Pitágoras:
h² + [(√2)/2]² = (√5)²
h² + 2/4 = 5
h² = 20/4 - 2/4
h² = 18/4
h = (3√2)/2
Finalmente, basta calcular a área:
A = ( 2√2 + √2) . (3√2)/2 . (1/2)
A = ( 3√2 ) . (3√2)/4
A = (9.2)/4
A = 9/2
A = 4,5 cm²
Alternativa correta é a letra a).
Aproveite e continue praticando com uma lista de exercícios resolvidos de geometria espacial.
Um forte abraço e bons estudos.