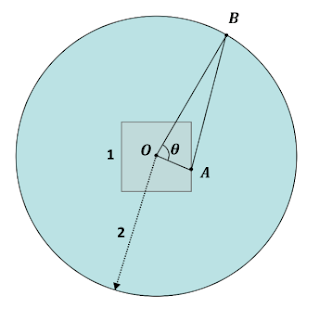
(FUVEST 2022) A figura mostra um quadrado e um círculo, ambos com centro no ponto 𝑂. O quadrado tem lado medindo 1 unidade de medida (u.m.) e o círculo tem raio igual a 2 u.m. O ponto 𝐴 está sobre o contorno do quadrado, o ponto 𝐵 está sobre o contorno do círculo, e o segmento 𝐴𝐵 tem tamanho 2 u.m.
Quando o ângulo 𝜃 = AÔB for máximo, seu cosseno será:
a) 1/8
b) 1/4
c) 1/2
d) (√2)/2
e) (√3)/2
Solução: questão de matemática da FUVEST 2022, prova aplicada no dia 12/12/2021.
Uma questão muito rica e interessante sobre geometria plana, envolvendo relações trigonométricas.
Em primeiro lugar, repare que o triângulo AOB é isósceles AB = OB = 2. Além disso, o segmento OA está limitado de (lado do quadrado/2) até (diagonal do quadrado/2), ou seja:
1/2 ≤ OA ≤ (√2)/2 [limitado a este intervalo]
A diagonal do quadrado de lado igual a L vale L√2.
Agora, surge uma pergunta: quando o ângulo 𝜃 = AÔB será máximo?
Quanto menor for o valor de OA, maior será o valor de 𝜃, podemos visualizar isso na ilustração a seguir:
Sendo assim, para termos o ângulo 𝜃 = AÔB no máximo, vamos trabalhar com OA = 1/2. Com isso, nosso objetivo é encontrar o cosseno de 𝜃 no triângulo a seguir:
cos 𝜃 = cateto adjacente/hipotenusa
cos 𝜃 = (1/4)/2
cos 𝜃 = (1/4) * (1/2)
cos 𝜃 = 1/8
Alternativa correta é a letra a).
Aproveite e continue praticando com uma lista de questões anteriores da FUVEST.
Um forte abraço e bons estudos.