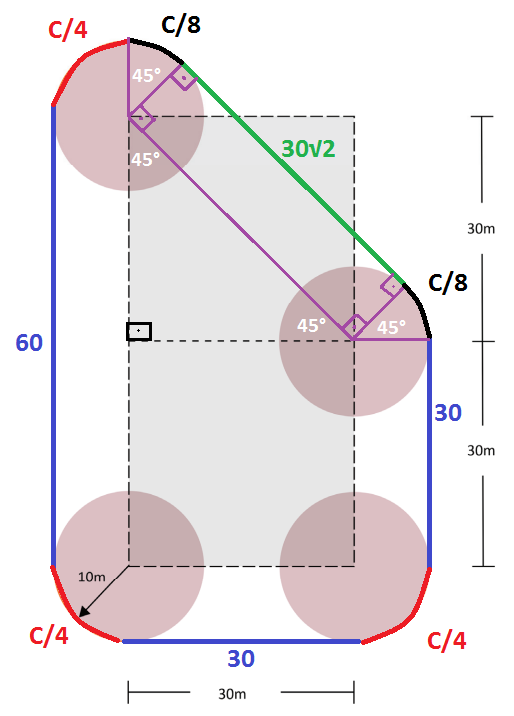
(FUVEST 2022) Quatro tanques cilíndricos são vistos de cima (em planta baixa) conforme a figura. Todos têm 10 m de raio e seus centros se posicionam em vértices dos dois quadrados tracejados adjacentes, ambos com 30 m de lado. Uma fita de isolamento, esticada e paralela ao solo, envolve os 4 tanques, dando uma volta completa (linha em laranja na figura).


O comprimento da fita, em metros, é: 

(A) 20𝜋 + 30(3 + √2)
(B) 20𝜋 + 30(4 + √2)
(C) 25𝜋 + 15(4 + √2)
(D) 25𝜋 + 30(4 + √2)
(E) 25𝜋 + 30(4 + 2√2)

Solução: questão de matemática da FUVEST 2022,  prova aplicada no dia 12/12/2021.

Vamos ilustrar os valores que compõem a fita.   Vamos considerar que C é o valor do comprimento da circunferência de raio (R) igual a 10 m.  Sabemos que:

C = 2𝜋R
C = 2𝜋10 m
C = 20𝜋 m


Em azul, temos as retas 60 + 30 + 30 = 120.

Em verde, temos a diagonal do quadrado de lado igual a 30. A diagonal do quadrado de lado 30 vale 30√2.

Em vermelho, temos 3 arcos que possuem ângulo de 90°, ou seja,  representam cada um, 1/4 da circunferência.  Somam juntos 3.(C/4)

Em preto, temos 2 arcos que possuem ângulo de 45°, ou seja, representam cada um, 1/8 da circunferência. Somam juntos 2.(C/8) = (C/4)

Agora, somamos os arcos em cor vermelha e cor preta.

3C/4 + C/4
4C/4
C

E sabemos que C = 20𝜋

Agora, somamos todos os valores encontrados:

120 + 30√2 + 20𝜋
30 (4 + √2) + 20𝜋
 
Alternativa correta é a letra b).

Aproveite e continue praticando com uma lista de questões anteriores da FUVEST.

Um forte abraço e bons estudos.