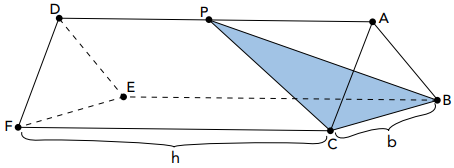
(UERJ 2018) A imagem a seguir ilustra um prisma triangular regular. Sua aresta da base mede b e sua aresta lateral mede h.
Esse prisma é seccionado por um plano BCP, de modo que o volume da pirâmide ABCP seja exatamente 1/9 do volume total do prisma.
Logo, a medida de AP é igual a:
a) h/9
b) h/3
c) 2h/3
d) 5h/6
Solução: questão de matemática do Vestibular UERJ 2018, prova do dia 17/09/2017.
Para resolvermos essa questão de geometria espacial, em primeiro lugar, precisamos ter em mente que o prisma triangular regular é um prisma reto e possui a base com o formato de um triângulo equilátero. Sabemos que a área do triângulo equilátero de lado igual a "b" vale (b² . √3)/4.
Atente também para o fato de que o objetivo da questão é unicamente encontrar a medida de AP e tanto o prisma quanto a pirâmide possuem a mesma base, sendo portanto desnecessário desenvolvermos a área do triângulo equilátero. Veremos isso no desenvolvimento da questão.
Vamos usar simplesmente a variável Sb para representar a área da base do prisma que é igual a área da base da pirâmide.
Como curiosidade, você pode conferir neste artigo: como calcular a área de um triângulo equilátero.
A fórmula do volume do prisma (Vprisma) é:
Vprisma = (área da base do prisma) x (altura do prisma)
Vprisma = Sb . h
A fórmula do volume da pirâmide (Vpirâmide) é:
Vpirâmide = (1/3) x (área da base da pirâmide) x (altura da pirâmide)
Vpirâmide = (1/3) . Sb . AP
O objetivo da questão é encontrar a medida do segmento AP de modo que o volume da pirâmide seja 1/9 do volume do prisma, vamos equacionar isto:
Vpirâmide = (1/9) Vprisma
9 . Vpirâmide = Vprisma
9 . (1/3) . Sb . AP = Sb . h
Repare que Sb está nos dois lados da equação e podemos, portanto, simplificá-lo. Daí o motivo de não ter sido necessário desenvolver a fórmula da área do triângulo equilátero.
3 . AP = h
AP = h/3
Alternativa correta é a letra b).
Aproveite e continue praticando com uma lista de questões de matemática da UERJ.
Um forte abraço e bons estudos.