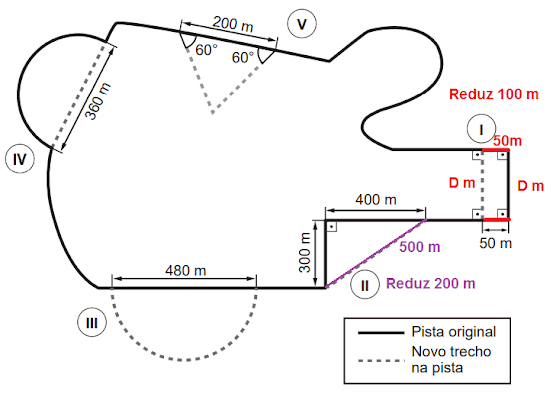
(ENEM 2022 Reaplicação/PPL) Para tornar uma pista de automobilismo mais segura, foram solicitadas intervenções em seu traçado.
Os engenheiros contratados elaboraram um projeto com cinco possíveis modificações, destacadas nos setores
(I), (II), (III), (IV) e (V) pelas linhas tracejadas, como mostra a figura. No entanto, na temporada atual, só é permitido
que se façam duas dessas alterações.
Todos os trechos passíveis de modificação, tanto no traçado original quanto no novo traçado, são semicircunferências ou segmentos de reta.
Pretende-se que a nova pista tenha extensão mais próxima que a da original após duas modificações. Os trechos
em comum da pista original e da nova pista não serão alterados.
Utilize 3 como aproximação para π.
Para atender às condições apresentadas, quais setores deverão ser modificados?
A) I e V
B) II e III
C) II e V
D) III e IV
E) IV e V
Solução: questão de matemática do ENEM 2022 - Reaplicação/PPL, prova aplicada no dia 11/01/2023.
Questão bem interessante de geometria plana do ENEM com aplicação prática da matemática no dia a dia. Note que das 5 alterações possíveis, exatamente 2 delas serão feitas de modo que a nova pista tenha extensão mais próxima que a da original após essas duas modificações.
Isto quer dizer que se existir uma alteração que, por exemplo, aumente em X metros a extensão da pista, e uma outra alteração que diminua em X metros essa extensão, então essas duas alterações juntas não irão mudar a extensão da pista, pois teremos um
+ X - X = 0 ( a extensão da pista não se altera)
Então, o que vamos fazer é buscar este caso nas alterações. Se não encontrarmos, tentaremos pegar aquelas duas que juntas resultem num valor de alteração de extensão da pista mais próximo de 0.
Nosso próximo desafio é encontrar as medidas dos segmentos identificados na figura do enunciado. Vamos fazer isso passo a passo, em cada uma das 5 modificações possíveis.
Modificação I
Note que a modificação I reduz em 100 m a extensão da pista (são aqueles dois trechos de 50 m reforçados em vermelho). Então guardamos assim:
I = - 100 m ( que representa que a modificação I irá reduzir a extensão da pista em 100m)
Note que a modificação II reduz 200 m, isto porque os dois trechos de 300 m e 400 m juntos totalizam 700 m, eles serão substituídos pela hipotenusa do triângulo retângulo, que vale 500 m. Você pode encontrar esse valor de 500 m aplicando o
Teorema de Pitágoras, ou então observando que estamos diante de um triângulo retângulo com medidas proporcionais a 3, 4 e 5. Então guardamos que
II = - 200 m
** Neste ponto, talvez você já tenha percebido, que a modificação V irá aumentar a extensão da pista em 200 m e o casamento da II com a V irá atender ao objetivo da questão. Mas como exercício, vamos seguir calculando.
Note que na modificação III, o novo trecho da pista é uma semicircunferência de raio igual a 240 m, sabemos que o comprimento (C) da circunferência é dado pela fórmula
C = 2 π R
Como é uma semicircunferência, então ficamos apenas com a metade, ou seja,
2πR = π R
2
O enunciado pede para adotar π = 3, de modo que a semicircunferência de raio igual a 240 m terá medida de 3 . (240) = 720 m. Perceba que o novo trecho da pista de 720 m substituirá o segmento de reta de 480m, de modo que essa alteração irá aumentar (720 - 480) = 240 m. Guardamos então a informação de que
III = + 240 m
Modificação IV
Note que na modificação IV, a semicircunferência de 540 m será trocada por uma reta de 360 m, o que vai gerar redução de extensão da pista de (540 - 360) = 180 m. Guardamos que
IV = - 180 m
Modificação V
Note que a modificação V aumenta em 200m a extensão da pista, para identificar isso, primeiro você precisa perceber que o triângulo ABC destacado na figura é um triângulo equilátero. Veja que os dois ângulos em A e C são de 60°, então o ângulo em B precisa ser de 60° também, isto porque a soma dos ângulos internos de um triângulo vale 180°.
60° + 60° + X = 180°
120° + X = 180°
X = 180° - 120°
X = 60°
O triângulo equilátero tem 3 ângulos internos de medida 60º e os três lados com a mesma medida.
Se o lado AC mede 200 m, então os lados AB e BC também medem 200 m. Note que o novo traçado da pista irá retirar o AC que mede 200m e acrescentar (AB + BC) que medem (200 + 200) = 400 m. Ou seja, a pista vai aumentar 400 - 200 = 200 m. Guardamos então a informação de que
V = + 200 m
Podemos perceber que para atingir o objetivo da questão, precisamos escolher as alterações II e V.
I = - 100 m
II = - 200 m
III = + 240 m
IV = - 180 m
V = + 200 m
Isto porque fazendo essas duas alterações, a pista irá continuar com a mesma extensão.
-200 + 200 = 0 ( e assim a pista continua com a mesma extensão anterior)
Podemos concluir que para atender às condições apresentadas, os setores II e V deverão ser modificados.
Alternativa correta é a letra c).
 Para tornar uma pista de automobilismo mais segura, foram solicitadas intervenções em seu traçado. Os engenheiros contratados elaboraram um projeto com cinco possíveis modificações, destacadas nos setores (I), (II), (III), (IV) e (V) pelas linhas tracejadas, como mostra a figura.){kind=link}
0 Comentários