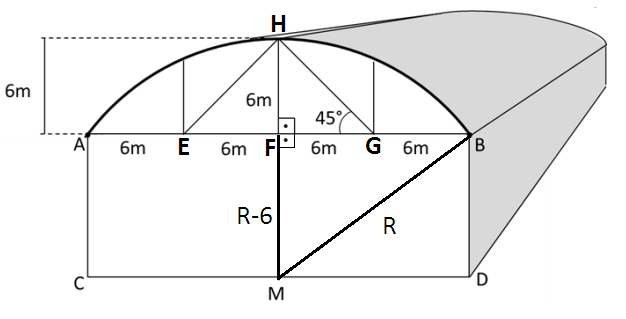
(UEG 2024/1) Para construir a cobertura do galpão esboçado na imagem ao lado, utilizou-se o formato de um arco de circunferência com centro no ponto médio (M) do segmento CD. Sabe-se, também, que, para fixação da estrutura metálica, o segmento AB foi dividido em quatro partes iguais. Considerando os dados da imagem ao lado e que o ângulo AMB é igual a 1,85 radianos (106º), o comprimento do arco que descreve a cobertura do galpão do ponto A ao ponto B é de
a) 27,75 m b) 28,75 m c) 24,75 m d) 26,75 m e) 25,75 m
Solução: questão de matemática do Vestibular da Universidade Estadual de Goiás (UEG), Processo Seletivo 2024/1, prova aplicada em 03/12/2023.
Para resolver essa questão de geometria plana, em primeiro lugar, vamos adicionar mais informações a essa figura:
A medida FH = 6m foi dada no enunciado.
Analisando o triângulo retângulo HFG, temos que FH = FG, isto porque
tg 45° = FH/FG
tg 45° = 1
1 = FH/FG
FH = FG
Sabemos que AE = EF = FG = GB
Como FH = FG = 6m, então temos que
AE = EF = FG = GB = 6m
No próximo passo, vamos obter a medida do raio R da circunferência, aplicando o Teorema de Pitágoras no triângulo retângulo MFB.
R² = (R-6)² + 12²
R² = R² - 12R + 36 + 12.12
12R = 3.12 + 12.12
R = 3 + 12
R = 15 m
O comprimento (S) do arco que descreve a cobertura do galpão do ponto A ao ponto B é de
S = α · R
S = 1,85 · 15
S = 27,75 m
Alternativa correta é a letra a).
Aproveite e continue praticando com uma lista de questões de matemática do Vestibular da UEG.
Um forte abraço e bons estudos.