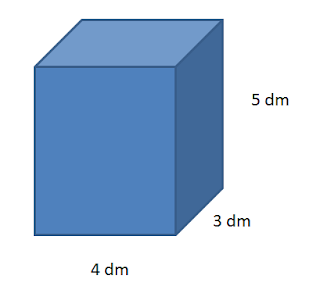
(EPCAR 2019) Um baú em forma de paralelepípedo reto retângulo pesa 20 kg e tem como medidas externas 50 cm de altura e 3 dm por 400 mm de base.
O baú contém uma substância homogênea que pesa 1,5 kg por litro e que ocupa o espaço correspondente a 90% do volume de um paralelepípedo reto retângulo de espessura desprezível e que possui as dimensões externas do baú.
Se o peso total do baú e da substância, em kg, é igual a x , então, pode-se dizer que x é um número natural
a) par menor que 100
b) ímpar menor que 100
c) primo.
d) divisível por 7 e maior que 100
Solução: questão de geometria espacial com muitas conversões de unidades de medida. Vamos usar todas as medidas do baú em decímetros.
A substância contida neste baú ocupa 90% dos 60 litros = 54 litros.
Ela pesa 1,5 Kg para cada litro, podemos fazer uma regra de três simples.
1,5 kg - 1 litro
S kg - 54 litros
S = 1,5 . 54
S = 81 kg
O peso do baú mais o peso da substância é de 20 + 81 = 101 kg. Agora, precisamos julgar as alternativas da questão:
a) par menor que 100 (FALSO)
b) ímpar menor que 100 (FALSO)
c) primo. (VERDADE)
d) divisível por 7 e maior que 100 (FALSO)
Um forte abraço e bons estudos.