(Colégio Naval 2020)
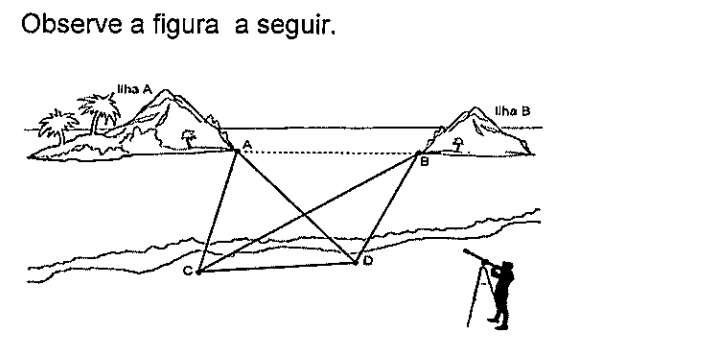
Um geógrafo posicionado numa praia deseja determinar a distância entre duas ilhas e para isso toma como referência os pontos A e B das ilhas como mostra a figura. Na praia ele marca dois pontos C e D distantes 70 m um do outro. Usando um medidor de ângulos (teodolito), os ângulos ACB = 38º, BCD = 37º, ADC = 60º e ADB = 53º. É correto afirmar que a distância entre os pontos A e B é:
Dados sen 37º = 3/5, sen 75º = 19/20, cos 53º = 3/5 e √2 = 7/5
a) maior do que 70 m e menor do que 75 m.
b) maior do que 75 m e menor do que 80 m.
c) maior do que 80 m e menor do que 85 m.
d) maior do que 85 m e menor do que 90 m.
e) maior do que 90 m e menor do que 95 m.
Aproveite e continue praticando com uma Lista de Exercícios Resolvidos de Lei dos Senos e Lei dos Cossenos.
Um forte abraço e bons estudos.