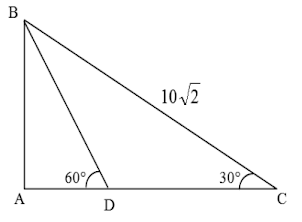
(EEAR CFS 1/2023) Seja ABC um triângulo retângulo em A, conforme a figura. Se D está em AC e se BC = 10√2 cm, então DC = ______ cm.

a) 3√6
b) 5√6
c) 5√6
      2
d) 10√6
        3

Solução: questão de matemática da EEAR (Escola de Especialistas da Aeronáutica) do Exame de Admissão ao CFS 1/2023. Prova aplicada no dia 05/06/2022.

Uma questão bem interessante de geometria plana, note que podemos encontrar a medida DC = x ilustrada na figura a seguir por meio da lei dos senos.

   10√2       =      x    
sen 120°         sen 30°

(10√2) . sen 30° = x . sen 120°

sen 120° = sen (180°-120°) = sen 60° = (√3)/2

sen 30° = 1/2

(10√2) . (1/2) = x . (√3)/2
10√2  = x.√3
x = 10√2
        √3 

Vamos racionalizar esta fração multiplicando-a por √3/√3.

x = 10√2  *  √3  
        √3           √3  
x = 10√6 
        3

Alternativa correta é a letra d).

Curiosidade:  você também pode calcular o valor de DC utilizando as relações trigonométricas no triângulo retângulo e o Teorema de Pitágoras.

Curiosidade2:  também é possível encontrar DC por meio da lei dos cossenos, note que o triângulo BDC é isósceles, pois os ângulos em B e em C são iguais, com isto BD = DC = x. Sendo assim, aplicando a lei dos cossenos, vamos encontrar x.

BC² = BD² + DC² - 2 . BD . DC . cos 120°
(10√2)² = x² + x² - 2 . x . x . (-cos 60°)
100 . 2 = 2x² - 2x² (-1/2)
100 . 2 = 3x²
x² = 100 . 2/3
x = 10√2
         √3
x = 10√2  *  √3  
          √3         √3

x =  10√6  
          3

Aproveite e continue praticando com uma lista de questões anteriores da EEAR. 

Um forte abraço e bons estudos.