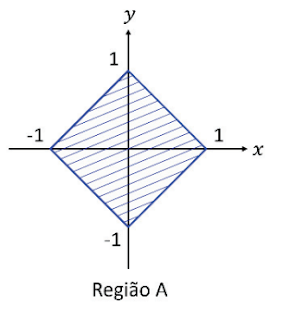
(FUVEST 2023) Considere a região do plano cartesiano
A = { (x , y) ∈ ℝ² : |x| + |y| ≤ 1 }
esboçada na figura.
Dado B = { (x , y) ∈ ℝ² : (x + 1)² + y² ≥ 1 } , a área da região A ∩ B é:
a) 2 - π/4
b) 2 - π/2
c) 4 + π/2
d) 4 - π/4
e) 2 + π/2
Solução: questão de matemática da FUVEST 2023, prova aplicada no dia 04/12/2022.
Uma questão muito rica e interessante envolvendo conceitos da geometria plana e da geometria analítica. Vamos resolvê-la passo a passo de forma ilustrada:
Em primeiro lugar, vamos esboçar a região B = { (x , y) ∈ ℝ² : (x + 1)² + y² ≥ 1 }
Iniciando por (x + 1)² + y² ≥ 1 , vamos trabalhar, num primeiro momento, apenas com
(x + 1)² + y² = 1
A equação acima representa uma circunferência com centro em (-1,0) e raio igual a 1.
Relembrando a equação reduzida da circunferência
(x - xc)² + (y - yc)² = R²
Coordenadas do centro da circunferência em (xc , yc) e raio R.
Vamos esboçar essa circunferência no plano cartesiano.
Já para esboçarmos (x + 1)² + y² ≥ 1 "atenção aí no sinal de ≥ " , teremos que colorir além da circunferência, a parte exterior à circunferência. Vamos atualizar a figura:
Note que a região B, ilustrada em azul, inclui também o desenho da circunferência (linha em azul mais escura). O que vamos fazer no próximo passo é trazer a região A para dentro dessa figura e ilustrar a região A ∩ B. Vamos fazer isso em dois passos.
Primeiro passo, ilustrando a região A junto com a região B.
Segundo passo, ilustrando em amarelo a região A ∩ B.
Agora, fica mais fácil visualizarmos que a área amarela é igual a área de um quadrado, menos a área de um setor circular (uma "fatia de pizza"). Mais precisamente, a área de um quadrado de lado √2 , menos a área de um setor circular com raio igual a 1 e ângulo central de 90° (pois coincide com um dos ângulos internos do quadrado que mede 90°). Nos próximos passos, vamos entender por que o lado do quadrado vale √2.
Podemos encontrar quanto vale o lado quadrado, representado por L, aplicando o Teorema de Pitágoras, repare na figura a seguir
L² = 1² + 1²
L² = 1 + 1
L² = 2
L = √2
E vamos aproveitar e calcular a área desse quadrado, que é igual a L².
Área do quadrado = L²
Área do quadrado = (√2)²
Área do quadrado = 2
Com estas informações, vamos atualizar a figura:
Como podemos calcular a área desse setor circular? Vamos utilizar a fórmula da área do setor circular.
Área do Setor = (ângulo central /360°) πR²
Área do Setor = (90° /360°) π(1)²
Área do Setor = (1/4) π
Área do Setor = π/4
Finalmente, já temos os elementos necessários para calcularmos a área da região A ∩ B.
Área de A ∩ B = (área do quadrado) - (área do setor)
Área de A ∩ B = 2 - π/4
Alternativa correta é a letra a).
Aproveite e continue praticando com uma lista de questões de matemática da FUVEST.
Um forte abraço e bons estudos.