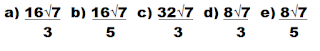Caro estudante,
Organizamos uma lista de exercícios resolvidos de Geometria Analítica. Algumas dessas questões são provenientes de questões de concursos militares e vestibular. As questões abordam os seguintes temas:
>> Equação da Circunferência;
>> Equação de reta, distância de um ponto a uma reta e distância entre duas retas paralelas;
>> Cônicas: Parábola, Elipse, Hipérbole e Circunferência.
Está preparado? Então, bons estudos com nossa bateria de questões sobre Geometria Analítica. Tente resolver as questões e depois confira a resolução de cada questão comentada com gabarito.
Questão 1 - (ENEM 2018) Um jogo pedagógico utiliza-se de uma interface algébrico-geométrica do seguinte modo: os alunos devem eliminar os pontos do plano cartesiano dando "tiros" seguindo trajetórias que devem passar pelos pontos escolhidos. Para dar os tiros, o aluno deve escrever em uma janela do programa a equação cartesiana de uma reta ou de uma circunferência que passa pelos pontos e pela origem do sistema de coordenadas. Se o tiro for dado por meio da equação da circunferência, cada ponto diferente da origem que for atingido vale 2 pontos. Se o tiro for dado por meio da equação de uma reta, cada ponto diferente da origem que for atingido vale 1 ponto. Em uma situação de jogo, ainda restam os seguintes pontos para serem eliminados: A(0;4), B(4;4), C(4;0), D(2;2) e E (0;2).
Passando pelo ponto A, qual equação forneceria a maior pontuação?
a) x = 0
b) y = 0
c) x² + y ² = 16
d) x² + (y - 2)² = 4
e) (x - 2)² + (y - 2)² = 8
Link para a solução da questão
Questão 2 - (ENEM 2017) A Igreja de São Francisco de Assis, obra arquitetônica modernista de Oscar Niemeyer, localizada na Lagoa da Pampulha, em Belo Horizonte, possui abóbadas parabólicas. A seta na Figura 1 ilustra uma das abóbadas da entrada principal da capela. A Figura 2 fornece uma vista frontal desta abóbada, com medidas hipotéticas para simplificar os cálculos.
Qual a medida da altura H, em metro, indicada na Figura 2?
a) 16/3 b) 31/5 c) 25/4 d) 25/3 e) 75/2
Link para a solução da questão
Questão 3 - (EsPCEx - 2018) Uma hipérbole tem focos F1 (-5,0) e F2 (5,0) e passa pelos pontos P(3,0) e Q(4,y), com y>0. O triângulo com vértices em F1, P e Q tem área igual a
Link para a solução da questão
Questão 4 - (Professor Docente I - Matemática - 2015 - Banca CEPERJ) A figura abaixo representa, no sistema de eixos cartesianos xoy, uma elipse de equação 16x² + 25y² = 400 e um triângulo AFG, retângulo em F.
Se AB é a medida do eixo maior dessa elipse e o ponto F um de seus focos, a área do triângulo AFG equivale a:
a) 8,0 b) 9,6 c) 12,8 d) 16,4 e) 20,0
Link para a solução da questão
Questão 5 - (Concurso Prefeitura de Araruama 2019 - Professor de Matemática - Banca: INCP) Determine o valor de f (235) - f (452), sabendo que f (1) = 5 e f (-3) = -7 são valores pertencentes à lei da função f(x) = a x + b:
a) 1.085
b) -1.085
c) 651
d) -651
e) -551
Link para a solução da questão
Questão 6 - (CEDERJ 2019.2) O conjunto de pontos (x, y) do IR² que satisfazem a equação x² + y² + y = 0 é uma
a) parábola que contém os pontos (0,0) e (1/2, - 1/2).
b) elipse com centro em (0,1/2).
c) circunferência de raio igual a 1/2.
d) hipérbole que contém os pontos (1/2, - 1/2) e (-1/2, - 1/2).
Link para a solução da questão
Questão 7 - (UNICAMP - 2020) Sabendo que 𝑐 é um número real, considere, no plano cartesiano, a circunferência de equação x² + y ² = 2𝑐𝑥. Se o centro dessa circunferência pertence à reta de equação x + 2y = 3, então seu raio é igual a
a) √2. b) √3. c) 2. d) 3.
Link para a solução da questão
Questão 8 - (Fuvest 2020) Um ponto (x,y) do plano cartesiano pertence ao conjunto F se é equidistante dos eixos OX e OY e pertence ao círculo de equação x² + y² -2x -6y +2 = 0. É correto afirmar que F
(A) é um conjunto vazio.
(B) tem exatamente 2 pontos, um no primeiro quadrante e outro no segundo quadrante.
(C) tem exatamente 2 pontos, ambos no primeiro quadrante.
(D) tem exatamente 3 pontos, sendo dois no primeiro quadrante e outro no segundo quadrante.
(E) tem exatamente 4 pontos, sendo dois no primeiro quadrante e dois no segundo quadrante.
Link para a solução da questão
Questão 9 - (EsPCEx - 2019) As equações das retas paralelas à reta r: 3x+4y-1=0, que cortam a circunferência λ: x²+y²-4x-2y-20=0 e determinam cordas de comprimento igual a 8, são, respectivamente
[A] 3x+4y+5=0 e 3x+4y+25=0.
[B] 3x+4y-5=0 e 3x+4y-25=0.
[C] 3x-4y+5=0 e 3x-4y+25=0.
[D] 3x+4y-5=0 e 3x+4y+25=0.
[E] 3x+4y+5=0 e 3x+4y-25=0.
Link para a solução da questão
Questão 10 - (FAMEMA 2022) A reta de equação x + 2y + 1 = 0 determina na circunferência ( x - 4)² + y² = 21 uma corda de comprimento igual a
(A) 8. (B) 7. (C) 6√3. (D) 6√2. (E) 4√5.
Link para a solução da questão
Questão 11 - (FAMERP 2020) Em um plano cartesiano, dois vértices de um triângulo equilátero estão sobre a reta de equação y = 2x – 2. O terceiro vértice desse triângulo está sobre a reta de equação y = 2x + 2. A altura desse triângulo, na mesma unidade de medida dos eixos cartesianos ortogonais, é igual a
a) (4√3)/5
b) (3√3)/4
c) (2√5)/5
d) (4√5)/5
e) (√3)/2