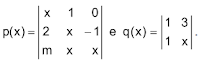| (Vunesp 2020) Considere os polinômios |
Para que p(x) seja divisível por q(x), é necessário que m seja igual a
(A) 30. (B) 12. (C) –12. (D) –3. (E) –30.
Solução: questão sobre polinômios da Vunesp que também envolve determinantes de matrizes.Por meio do método de Sarrus, podemos desenvolver o determinante de ordem 3 e encontrar que p(x) = x³ + x² - 2x - m
Desenvolvendo o determinante de ordem 2 encontraremos q(x) = x-3
O objetivo da questão é encontrar o valor de m de modo que p(x) seja divisível por q(x).
Repare que q(x) é um polinômio de grau 1, logo, pelo Teorema do Resto, se aplicarmos a raiz de q(x) no polinômio p(x) o resultado será o seu resto e que este deverá ser 0.
P ( raiz de q(x) ) = Resto = 0
A raiz de q(x) vale 3 , já que x-3 = 0 // x = 3.
P ( 3) = 0 = 3³ + 3² - 2.3 - m = 0
27 + 9 -6 = m
m = 30 [Alternativa correta é a letra A]
Curiosidade: e se eu não me lembrar do Teorema do Resto? Basta desenvolver a divisão do polinômio p(x) por q(x) e ao final igualar o resto encontrado a zero. Será um método um pouco mais demorado. Fiz manualmente numa folha de papel, veja a seguir:
Ainda têm dificuldades em fazer a divisão de polinômios? Confira nessa questão do Cederj uma divisão de polinômios feita passo a passo.
Aproveite e confira também uma questão da EsPCEx 2019 sobre polinômios, divisibilidade e resto.
Um forte abraço e bons estudos.