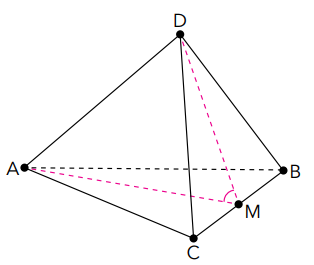
(UERJ 2017) Uma pirâmide com exatamente seis arestas congruentes é denominada tetraedro regular. Admita que a aresta do tetraedro regular ilustrado a seguir, de vértices ABCD, mede 6 cm e que o ponto médio da aresta BC é M.
O cosseno do ângulo AMD equivale a:
a) 1/2
b) 1/3
c) 2/3
d) 2/5
Solução: questão de matemática do Vestibular UERJ 2017, prova do dia 16/10/2016 (2° Exame de Qualificação).
Uma questão muito interessante de geometria espacial sobre o tetraedro regular, onde utilizaremos também a lei dos cossenos.
O tetraedro regular é formado por 4 faces, as quais são triângulos equiláteros (com os 3 lados iguais).
Olhando para o triângulo BCD, perceba que o segmento DM é a mediana relativa ao lado BC. A mediana é o segmento de reta que parte de um vértice do triângulo e alcança o ponto médio do lado oposto. Além disso, no triângulo equilátero, a altura, mediana e bissetriz, referente a cada lado, estão sobre a mesma reta. Logo, DM é a altura do triângulo equilátero BCD que possui três lados iguais a 6.
Sabemos que a altura de um triângulo equilátero vale (Lado . √3 ) / 2 = (6√3)/2 = 3√3
>> Caso necessário, faça por aqui uma revisão sobre: como calcular a área e altura de um triângulo equilátero.
Sabemos que DM = 3√3 e além disso, podemos visualizar que AM = 3√3. Isto porque AM é a altura do triângulo equilátero ABC que também tem lado igual a 6. Vamos atualizar a figura com essas informações.
Note que o cosseno do ângulo AMD, que foi representado por θ, pode ser encontrado por meio da lei dos cossenos:
6² = (3√3)² + (3√3)² - 2 . (3√3) . (3√3) . cos θ
36 = 9.3 + 9.3 - 2 . 9 . 3 . cos θ
36 = 27 + 27 - 54 . cos θ
36 = 54 - 54 . cos θ
36 - 54 = -54 . cos θ
-18 = -54 . cos θ
cos θ = -18 / -54
cos θ = 1/3
Alternativa correta é a letra b).
Aproveite e continue praticando com uma lista de questões de matemática da UERJ.
Um forte abraço e bons estudos.