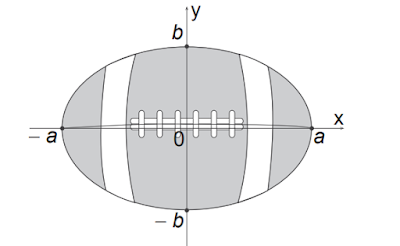
( EsPCEx 2023 )  A fim de proporcionar a seus militares melhores condições para a prática de Treinamento Físico Militar, um Batalhão do Exército Brasileiro planeja construir uma pista de corrida.  Sabe-se que a pista deverá ser limitada por duas elipses, conforme ilustrado pela figura abaixo.  A largura da pista ainda será definida, mas já existe a determinação de que a distância de P1 a P2 seja de 120 metros.  Planeja-se também instalar um mastro em cada foco da elipse interior, representados na figura pelos pontos R1 e R2, para que posteriormente o Batalhão possa hastear bandeiras.  A ordem é que os mastros possuam a distância de 80 metros entre si.  Considere a equação da elipse interior como x² + y² = 1. a²    b² Assinale a alternativa que contém o valor, em metros, de a+b : a) 60 + 20√5 b) 60 + 40√5 c) 60 + 100√5 d) 40 e) 80 Solução:  questão de matemática da  EsPCEx (Concurso de Admissão à Escola Preparatória de Cadetes do E...

(Escola de Aprendizes-Marinheiros 2023)  Considere as equações  x² - 9y² - 6x - 18y - 9 = 0,  x² + y² - 2x + 4y + 1 = 0  e   x² - 4x - 4y + 8 = 0 ,  com (x,y) ∈ ℝ².  Analise e assinale a opção que apresenta, respectivamente, as representações geométricas das equações. a) Hipérbole, elipse, parábola. b) Hipérbole, circunferência, reta. c) Hipérbole, circunferência, parábola. d) Elipse, circunferência, parábola. e) Elipse, circunferência, reta. Solução:  questão de matemática do Concurso Público de Admissão às Escolas de Aprendizes-Marinheiros/CPAEAM/2023,  prova do dia 02/04/2023. Analisando cada equação, temos que: 1) x² - 9y² - 6x - 18y - 9 = 0 De acordo com as alternativas de resposta, a primeira equação só pode ser hipérbole ou elipse.  Note que os sinais trocados dos coeficientes que multiplicam x² e y² nos indicam que não será elipse, então só pode ser hipérbole.  Vamos obter a equação dessa hipérbole para co...

(Escola de Aprendizes-Marinheiros 2022) Considere a elipse E com centro na origem, um dos focos em F1(0, √(2/3)) e que passa pelo ponto P (1/2, 1/2), como mostrado na figura abaixo.  Assinale a opção correta que apresenta a excentricidade de E . a) 1/6 b) 1/2 c) √(2/3) d) 1 e) √(3/2) Solução:  questão de matemática do Concurso Público de Admissão às Escolas de Aprendizes-Marinheiros/CPAEAM/2022,  prova aplicada no dia 05/06/2022. A equação reduzida desta elipse, com foco sobre o eixo y, é dada por: (x²/b²) + (y²/a²) = 1 Sabemos que P (1/2, 1/2) é um ponto da elipse, sendo assim, vamos aplicá-lo na equação. ((1/2)²/b²) + ((1/2)²/a²) = 1 ((1/4)/b²) + ((1/4)/a²) = 1 (1/4b²) + (1/4a²) = 1 (a²+b²) / (4b²a²) = 1 a² + b² = 4b²a² (Equação I) Também sabemos que c² = a² - b²  e que o valor de c nesta elipse é igual a √(2/3) c² = a² - b² [√(2/3)]² = a² - b² 2/3 = a² - b² b² = a² - 2/3 (Equação II) Agora, aplicamos II em I. a² + (a² - 2/3) = 4(a² - 2/3)a² 2a² - 2...

(Escola de Aprendizes-Marinheiros 2022) Determine a equação reduzida da elipse cujo eixo menor tem por extremos os focos da hipérbole x² - y² = -1 e cuja excentricidade é o inverso da excentricidade da hipérbole dada, como mostra a figura abaixo, e assinale a opção correta. Solução:  questão de matemática do Concurso Público de Admissão às Escolas de Aprendizes-Marinheiros/CPAEAM/2022,  prova aplicada no dia 05/06/2022. Uma questão muito interessante de geometria analítica envolvendo duas cônicas: hipérbole e a elipse. Primeiramente, vamos trabalhar na hipérbole, podemos notar que o eixo real está em y, logo temos a seguinte estrutura. O enunciado nos forneceu a equação da hipérbole como sendo x² - y² = -1 , vamos multiplicar os dois lados da equação por -1. Fazendo isso, chegaremos à seguinte equação reduzida da hipérbole. y² - x² = 1 Como a equação reduzida da hipérbole tem a forma:   (y²/a²) - (x²/b²) = 1 então a² =1 e b² = 1  e com eles podemos enc...

(UECE 2022.1)  Sabe-se que, no sistema solar, os planetas giram em torno do Sol e que a órbita de cada um deles é uma elipse tendo o Sol como um dos focos. O planeta (ou planetoide) Plutão é o mais distante do Sol. No entanto, esta distância não é constante, pois sua órbita é uma elipse. A excentricidade de uma elipse é definida como a divisão do comprimento da distância focal (2𝑐), pelo comprimento do eixo maior (2𝑎) da elipse 2𝑐/2𝑎 = 𝑐/𝑎 . Quanto maior a excentricidade, mais alongada é a elipse. Sabendo que a maior distância de Plutão ao Sol é aproximadamente 7 u.a. e a menor é aproximadamente 4 u.a., é correto dizer que a medida da excentricidade da órbita de Plutão é aproximadamente  A) 0,273. B) 0,258. C) 0,260. D) 0,232. u.a. ≡ unidade astronômica. Solução:  questão de matemática do Vestibular da Universidade Estadual do Ceará (UECE) 2022.1,  prova de conhecimentos gerais da 1ª Fase, aplicada no dia 15/11/2021. Na figura a seguir, vamos ilustrar ...

(ENEM 2015) A figura representa a vista superior de uma bola de futebol americano, cuja forma é um elipsoide obtido pela rotação de uma elipse em torno do eixo das abscissas.  Os valores a e b são, respectivamente, a metade do seu comprimento horizontal e a metade do seu comprimento vertical.  Para essa bola, a diferença entre os comprimentos horizontal e vertical é igual à metade do comprimento vertical. Considere que o volume aproximado dessa bola é dado por V = 4ab².   O volume dessa bola, em função apenas de b, é dado por a) 8b³   b) 6b³   c) 5b³   d) 4b³   e) 2b³ Solução: vamos aplicar a relação dada no enunciado: " a diferença entre os comprimentos horizontal e vertical é igual à metade do comprimento vertical. " 2a - 2b = 1/2 . 2b 2a  = b  + 2b 2a = 3b a = 3b/2 Agora, basta aplicar o valor de a em função de b na fórmula V = 4ab² para encontrarmos V em função apenas de b. V = 4ab² V = 4( 3b/2 )b² V = 6b³ Al...

(Professor Docente I - Matemática - 2015 - Banca CEPERJ)  A figura abaixo representa, no sistema de eixos cartesianos xoy, uma elipse de equação 16x² + 25y² = 400 e um triângulo AFG, retângulo em F. Se AB é a medida do eixo maior dessa elipse e o ponto F um de seus focos, a área do triângulo AFG equivale a: a) 8,0 b) 9,6 c) 12,8 d) 16,4 e) 20,0 Solução: questão sobre cônicas - elipses do último concurso para professor de matemática do Estado do RJ.  As fórmulas desta elipse são x²/a² + y²/b² = 1     c² = a² - b²   c é a distância focal A partir desta equação inicial dada 16x² + 25y² = 400 podemos dividir ambos os lados da equação por 400, mantendo assim a igualdade. (16x² + 25y² ) / 400 = 400 / 400 16/400 x² + 25/400 y² = 1 x² /25 + y² / 16 = 1 Temos que a² = 25 e b² = 16 a =  ± 5  e b = ± 4 Podemos agora encontrar a distância focal c² = 25 - 16 = 9 c = ± 3 Por último, precisamos...